Στον συναρπαστικό κόσμο των τυχερών παιχνιδιών και στις επενδύσεις, η λήψη της σωστής απόφασης μπορεί συχνά να μοιάζει με ένα παιχνίδι υψηλού κινδύνου. Το Κριτήριο Kelly, που αναπτύχθηκε από τον John L. Kelly Jr. το 1956, ξεχωρίζει ως μια επαναστατική φόρμουλα για τους παίκτες, επενδυτές και ριψοκίνδυνους. Ωστόσο, παρά τις ισχυρές δυνατότητές του, πολλά άτομα δυσκολεύονται να κατανοήσουν και να το εφαρμόσουν στη πράξη.
Το κριτήριο Kelly προσφέρει μια μαθηματική προσέγγιση που έχει σχεδιαστεί για να σας βοηθήσει να διαχειριστείτε τα στοιχήματά σας, μεγιστοποιώντας τα πιθανά κέρδη σας και ελαχιστοποιώντας τους κινδύνους σας. Είναι μία φόρμουλα η οποία δείχνει πόσο πρέπει να είναι το ποσό πονταρίσματος σε μια σειρά από παίγνια, στα οποία το αποτέλεσμα τους βασίζεται σε πιθανοθεωρητικό μοντέλο, και αυτό προκύπτει στη θεωρία πιθανατήτων, οικονομικά, στις μετοχές, (τι ειναι το χρηματιστηριο)κτλ.
Με αυτή τη φόρμουλα μπορούμε να καθορίσουμε το ποσό πονταρίσματος και να κερδίσουμε σχεδόν βέβαια σε μια σειρά από επαναλλαμβανόμενα στη θεωρία παιγνίων υπό την προϋποθεση ότι το αποτέλεσμα δεν είναι ισοπίθανα γεγονότα.
Κριτήριο kelly
Για παράδειγμα αν βρεθεί ένα παίγνιο στο οποίο η πιθανότητας νίκης είναι μεγαλύτερη του 50% πχ 52%, 53% κτλ για δηλαδή για πιθανότητα νίκης είναι 60% και 40%. Η πιθανότητα των υπόλοιπων ενδεχομένων είναι μικρότερη, έχοντας αρχικό κεφάλαιο για παράδειγμα 100 ευρώ, τότε ποσό του πονταρίσματος πρέπει να είναι(60%-40%) = 20% του αρχικού κεφαλαίου δηλαδή 20Ε.
Στη συνέχεια ανάλογα σε κάθε βήμα είτε χάνει είτε ερδίζει πρέπει να γίνεται αναπροσρμογή του ποσού ,βέβαια η παραπάνω περίπτωση εφαρμόζεται στη περίπτωση που τα odds είναι 1-1. Η γενική formula όπου μπορείτε να υπολογίσετε με σύνθετα odds όπως 1-2 είναι η παρακάτω.
Γενική Formula
Kbet = (p(b+1)-1)/b
Kbet το ποσό από το αρχικό ποσό που θα ποντάρουμε
p πιθανότητα νίκης
1-p πιθανότητα ήττας
b τα odds
λίγη Ιστορία από τα Bell Labs
Αυτή η απλή μαθηματική φόρμουλα δημιουργήθηκε από τον John Larry Kelly, ο οποίος ήταν φυσικός και οποίος δούλευε στα Bell Labs. Υπάρχει αυστηρά μαθηματική όπου αναλύεται στo paper "A new Interpretation of Information Rate" του Bell System Technical Journal.
Η όλη ιδέα βασίζεται πάνω στην έννοια της εντροπίας για τη ποσοτικοποίηση της πληροφορίας, η οποία προήλθε από Claud Shannon. Στο paper του 1948 A Mathematical Theory of Communication, Claude Shannon έκανε εισαγωγή στο τι είναι η έννοια εντροπία της πληρoφορίας.
δειτε το παρακάτω video για να καταλάβετε διαισθητικά πως λειτουργεί η έννοια της εντροπίας https://youtu.be/9r7FIXEAGvs
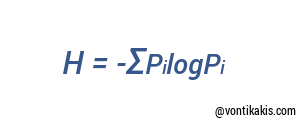
Συμπέρασμα
Η ίδια η φόρμουλα μπορεί να εφαρμοστεί στα τυχερά παίγνια, επίσης χρησιμοποιείται στα χρηματοοικονομικά και συστήματα money management κτλ. Εκτός απο τις επενδύσεις που βασίζονται σε υψηλό ρίσκο πάντα μπορείτε να χρησιμοποιήσετε χρονική αξία του χρήματος για να υπολογίσετε μια σταθερή μελλοντική απόδοση.
